Math

[Math] 벡터의 내적(Dot Product)과 외적(Cross Product)

devfactory 2024. 9. 30. 00:55

내적(Dot Product)

두 벡터의 내적은 두 벡터의 크기와 방향의 유사성을 측정하여 하나의 스칼라값을 구하는 연산이다.

1) a⋅b=a1​×b1​+a2​×b2

2) A⋅B=∣A∣∣B∣cosθ

벡터 a=와 b=의 내적은 다음과 같다.

a⋅b=2​×3​+1​×0 = 6

V1을 V2에 투영한 값(2) * V2의 길이(3) = 내적값

특징

  • 스칼라 값을 반환한다.
  • 교환법칙이 성립한다.
  • 두 벡터가 이루는 각도에 따른 내적 값
    • 0도일 때 (같은 방향일 때) 벡터의 크기의 곱
    • 90도일 때 (서로 수직) 0
  • 두 벡터가 반대 방향(90도를 초과해서 차이날 때)일 때는 음수 값을 반환한다.

활용

  • 시야(FOV: Field of View)계산
    내적을 통해 적이 시야 내에 있는지 확인 할 수 있다.
bool Fov(Vector3 originPosition, Vector3 direction, Vector3 targetPosition, float angle)
{
    const double deg2Rad = Math.PI / 180f;
    var dotProduct = Dot(direction, targetPosition - originPosition);

    return dotProduct > Math.Cos(deg2Rad * angle * 0.5f);
}

float Dot(Vector3 v1, Vector3 v2)
{
    return (v1.x * v2.x) + (v1.y * v2.y) + (v1.z * v2.z);
}

 

  • 매개변수
    • originPosition 관찰자의 위치
    • direction: 관찰자의 방향벡터
    • targetPosition: Target의 위치.
    • angle: 관찰자의 시야각 (도 단위).
  • 계산 과정
    • deg2Rad: 각도를 라디안으로 변환하기 위한 상수.
    • dotProduct: 관찰자의 방향벡터와 관찰자에서 Target으로의 방향벡터(그림의 targetdirection)에 대한 내적을 계산한다.
    • 계산된 내적 값이 주어진 각도의 코사인 값의 절반(시야를 좌 우측으로 나누기에 절반으로 나줘준다.)보다 큰지를 비교하여 true 또는 false를 반환. 이 조건은 대상이 시야각 내에 있는지를 판별한다.

 

 

FOV 계산

 

 

 

 

외적(Cross Product)

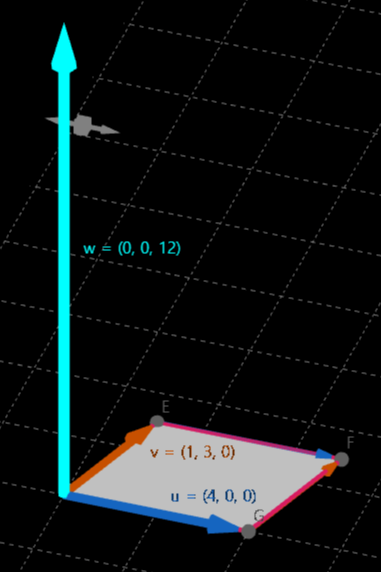
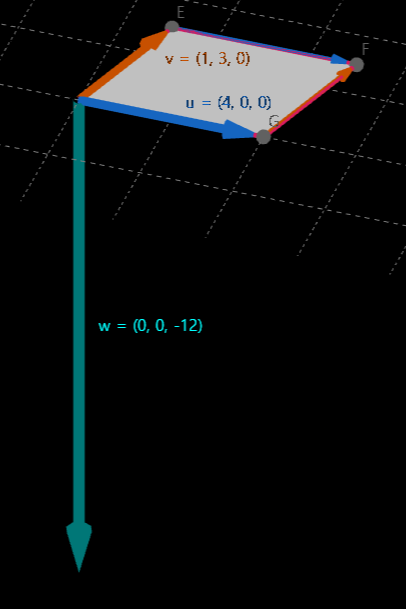
두 벡터의 외적은 두 벡터에 수직인 새로운 벡터를 생성한다.

벡터 a=[a1,a2,a3]와 b=[b1,b2,b3]의 외적은 다음과 같이 계산된다.

1) A×B = [A2​×B3​−A3​×B2​,A3​×B1​−A1​×B3​,A1​×B2​−A2​×B1​]

2) A×B=∣A∣∣B∣sinθ

 

특징

  • 벡터 값을 반환한다.
  • 반환된 벡터는 두 벡터에 수직한다.
  • 벡터의 크기는 두 벡터가 이루는 평행사변형의 넓이와 같다.
  • 두 벡터가 평행하면 외적은 0 벡터가 된다.

U x V(좌) V x U(우)

활용

  • 평면의 법선 벡터 구하기(그래픽에서 많이 사용된다.)
  • 한 오브젝트를 기준으로 다른 오브젝트의 좌우관계 파악하기
string GetLeftRightRelation(Vector3 origin, Vector3 direction, Vector3 target)
{
    Vector3 vectorToTarget = target - origin;

    Vector3 crossProduct = Vector3.Cross(direction, vectorToTarget);

    // Z축 비교
    if (crossProduct.Z > 0)
    {
        return "left";
    }
    else if (crossProduct.Z < 0)
    {
        return "right";
    }
    else
    {
        return "forward";
    }
}

Vector3 Cross(Vector3 a, Vector3 b)
{
    return new Vector3(
        a.Y * b.Z - a.Z * b.Y,
        a.Z * b.X - a.X * b.Z,
        a.X * b.Y - a.Y * b.X
    );
}

두 벡터를 외적하면 시계방향의 경우 음수 반시계 방향은 양수가 나오는 점을 이용해 좌우측중 어디에 위치했는지 알 수 있다.

반응형