1. 행렬의 정의
수 또는 대수를 직사각형 형태로 나열한 것
각 요소는 행렬의 특정 위치에 있는 값으로 정의되며 다음과 같이 표현된다.
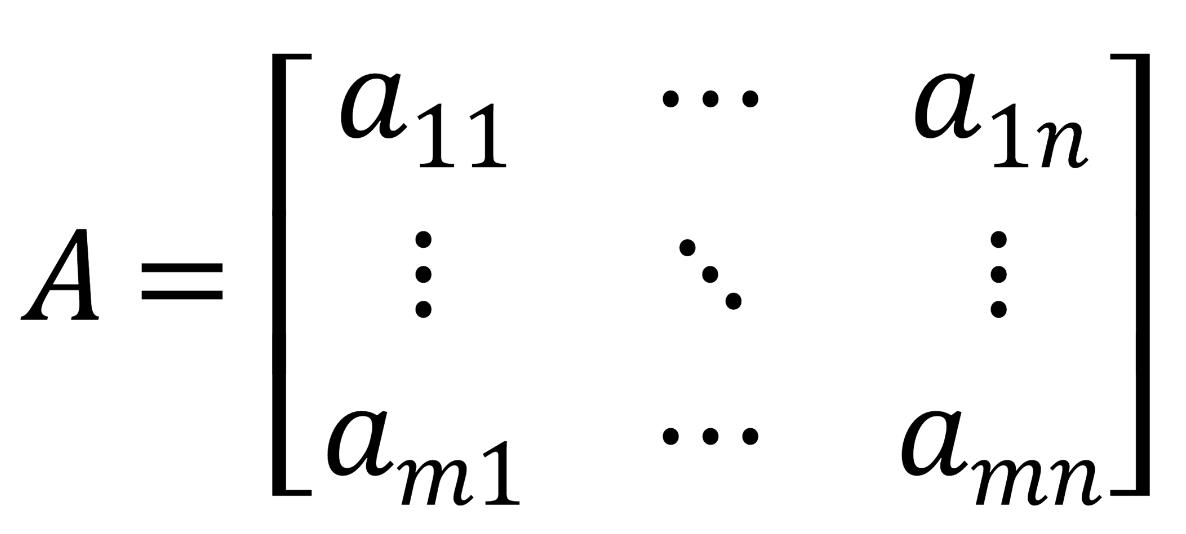
여기서 aij는 i번째 행과 j번째 열의 요소를 나타낸다.

예를 들어 위의 행렬은 3X2 행렬이며 (3, 1) 성분은 e가 된다.
2. 행렬의 종류
정방행렬(square matrix)
행과 열의 수가 같은 행렬

영행렬(zero matrix)
모든 요소가 0인 행렬

대각행렬(diagonal matrix)
주대각선을 제외한 요소가 모두 0인 정사각형 행렬

단위행렬 · 항등행렬(unit matrix · identity matrix)
주대각선 요소가 모두 1이고 나머지 요소가 0인 정사각형 행렬

전치행렬(transposed matrix)
행과 열을 교환하여 얻는 행렬
즉, 주대각선을 축으로 하는 반사 대칭을 가하여 얻는 행렬
기호는 AT를 사용한다.
m×n 행렬의 전치행렬은 n×m 행렬이 된다.
(AT)T = A가 성립한다.
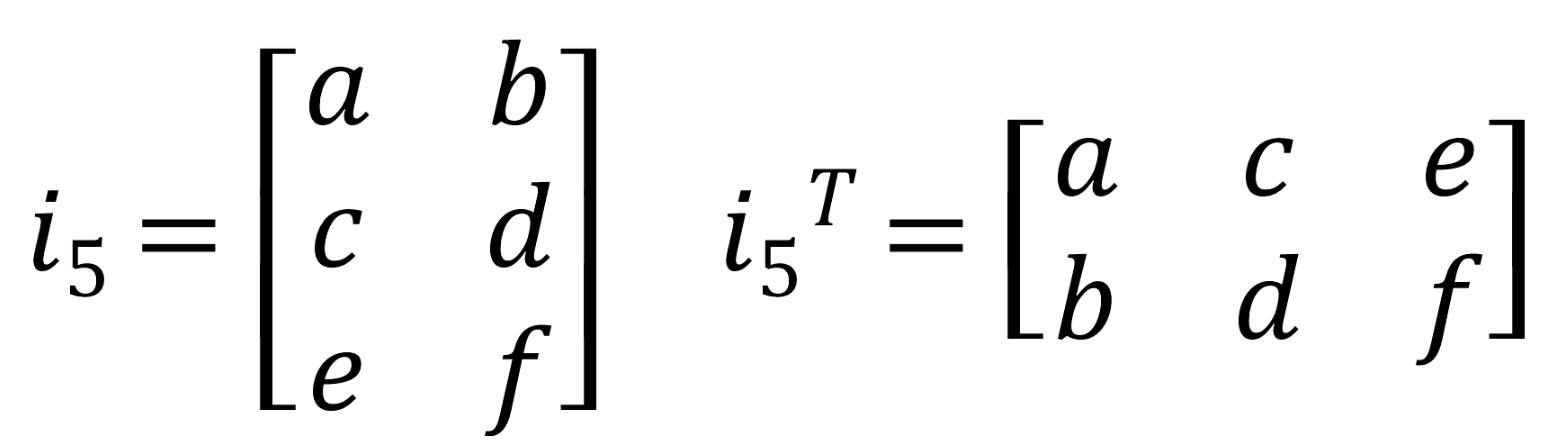
대칭행렬(symmetric matrix)
자신의 전치행렬이 자신과 같은 행렬
즉, row와 column이 바뀌어도 동일한 값을 가지는 행렬 (i6 12 = i6 12)

회전변환행렬(Rotation matrix)
임의의 행렬을 원점을 중심으로 회전시키는 행렬으로 선형변환의 성질 중 하나이다.
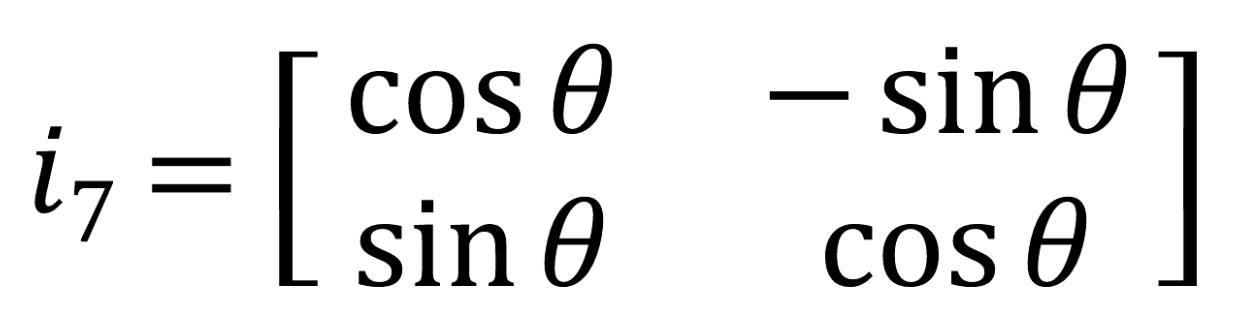
역행렬(inverse matrix)
어떤 정사각 행렬에 대해, 그 행렬을 곱했을 때 단위행렬이 되는 행렬을 의미한다.
기호는 A-1을 사용한다.
3. 행렬의 연산
덧셈과 뺄셈
- 행렬의 덧셈과 뺄셈은 행렬의 같은 위치의 요소끼리 더하거나 빼면 된다.
- 행렬의 차원이 같아야만 연산이 가능하다.
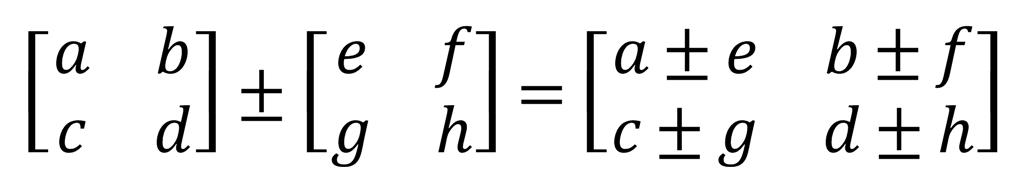
스칼라곱
- 행렬의 스칼라곱은 행렬의 모든 요소에 각각 스칼라를 곱하면 된다.
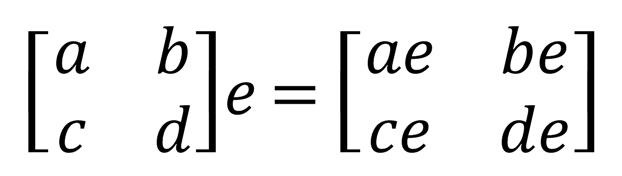
행렬의 곱
- 행렬 A * B가 정의되기 위해서는 A의 열 수와 B의 행수가 같아야 한다.
- A가 m * n, B가 n * p크기의 행렬이라면 결과 행렬의 크기는 m * p가 된다.
- A * B = C에서 결과행렬 C의 (i, j) 성분은 A의 i행과 B의 j열의 내적값이다.


역행렬
- 역행렬이 존재하려면 행렬의 크기는 n*n의 정사각형 행렬이어야 한다.
- 행렬식이 0이 아니어야 한다. 행렬식이 0인 경우 특이행렬이라 하며 역행렬이 존재하지 않는다.
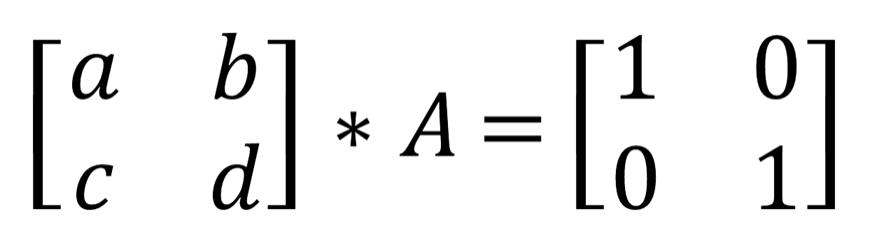
위의 식을 만족하는 행렬 A가 앞의 행렬의 역행렬이 된다.

위의 식을 다음과 같이 변형하면 a, b, c, d의 값을 찾기 위해서 연립방정식을 사용할 수 있다.

즉 다음과 같은 연립방정식이 나온다
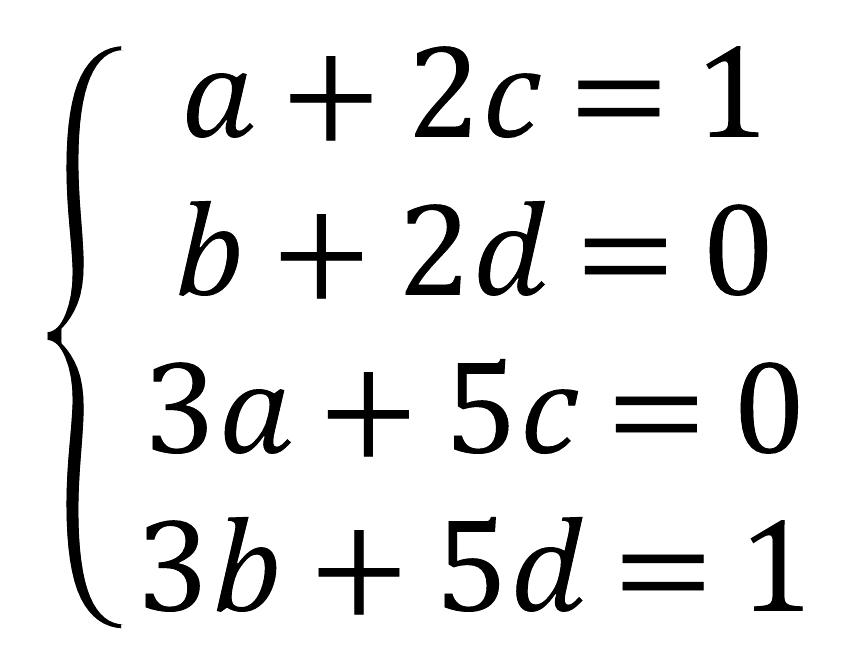
이를 계산하면 아래의 값이 나온다.
a = -5
b = 2
c = 3
d = -1
즉 역행렬은 다음 값이 된다.
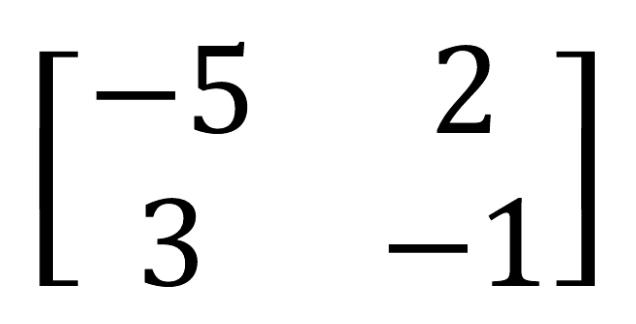
'Math' 카테고리의 다른 글
| [Math] 선형 변환 (0) | 2024.11.21 |
|---|---|
| [Math] 스팬과 선형종속 (1) | 2024.11.15 |
| [Math] 벡터의 일차 결합 (0) | 2024.10.10 |
| [Math] 벡터의 내적(Dot Product)과 외적(Cross Product) (0) | 2024.09.30 |
| [Math] 벡터 (Vector)와 스칼라(Scala) (1) | 2024.09.30 |



